因果推論とは
入力データ（インプット）と出力データ（アウトプット）から、その因果関係（原因とそれによって生じる結果との関係）を統計的に推定していく考え方のこと。統計的因果推論とも言われる。因果推論を用いた政策効果の測定がノーベル経済学賞を受賞したこともあり、近年注目されている手法。
統計学では複数のデータの“相関関係”を分析する手法が中心でした。検定や回帰などの手法は、データの関係がどれぐらい強いのかを表す分析手法です。しかし、これらの手法では、“相関”があることはわかりますが、“因果”がわかりません。そのため、因果関係を推計する「因果推論」が注目されるようになりました。
因果関係を分析する事例として、広告効果の推計があげられます。広告に接触することで商品（例えばエアコンやアイスなど）の購入率が上がったとしましょう。この場合でも、商品を購入したという「結果」が、広告に接触したという「原因」だけで、すべて説明することはできません。広告に接触したことよりも、店頭で安売りしていたことが影響したかもしれません。あるいは単純に気温が高くなったから買っただけの可能性もあります。
この場合、実際に広告に接触した人が「もし、接触しなかったら」どうなっていたのかを把握することで、因果関係を推計することができます。接触‘した’場合の効果と、接触‘しなかった’場合の効果を比較すれば、その差が因果関係の割合と考えられるのです。
言い換えると、「もし、◯◯だったら」どうなっていたのかを、いかに推計できるかが因果推論のポイントとなります。広告に接触した人が接触していなかったら、薬を服用した患者が服用していなかったら、政策の対象となる住民が対象外になっていたら、などを推計することです。
因果推論の考え方
統計的に因果関係を分析するためには、一人の変化ではなく、複数名（集団）の変化をもとに、因果関係を推計します。広告の効果の例でいえば、広告に接触した人（処置群）と、接触しなかった人（対照群）について、その広告の商品を購入した割合を比較して、広告の効果を推計します。実際には広告に接触しなかった人（対照群）のデータから、広告に接触した人（処置群）が、広告に‘接触しない場合’の効果を推計します。
一般的に、広告に接触する割合は女性で高いと言われており、広告の効果なのか、性別の影響なのかを特定できません。そのため、広告の接触・非接触以外の条件を同一にして、処置群と対照群を比較します。具体的には、各群に入る対象者の偏りを補正することで、処置群と対照群を対等に比較することができ、処置群における効果を推計することが可能になります。
しかし、すべての条件（要素）を統一することは現実的ではありません。そのため、広告効果の例でいえば、商品の購買に影響を及ぼすと考えられる要素（性別、年齢、職業、収入など）を特定し、それらの要素について偏りを補正することが重要になります。
まとめると「因果推論」のポイントとしては以下のことが挙げられます。
①処置群と対照群の結果から、処置群における「もし、◯◯だったら」の効果を推計する
②処置群と対照群のサンプル構成は◯◯以外の要素は同一になるよう補正する
③すべての要素を同一にできないため、結果に影響を及ぼす重要な要素を抽出する
因果推論における偏り補正の進め方
各群に含まれる対象者の偏りを統計的に補正することが「因果推論」でのポイントとなります。偏りを補正する代表的な２つの手法を紹介します。
①差分の差分法（Difference in differences）
事象が発生する前の水準を考慮して、対象者の偏りを補正する方法です。広告効果の推計で考えると、広告に接触した群の商品購入率の「増加分（差分）」と、接触しなかった群の「増加分（差分）」を求め、さらに「差分（差分の差分）」をとって、広告の効果を推計します。
グラフをみると広告の出稿がある前の段階から、商品購入率に差があることがわかります。広告に接触する群は事前段階から商品購入率が高く、言い換えると、広告に接触するような人は、接触する前から、商品購買などに積極的な人が多いという“偏り”があるとも言えます。事前段階の水準を考慮して、その水準から増分をもとに効果を推計することで、対象者の偏りをできるだけ取り除こうという考え方です。
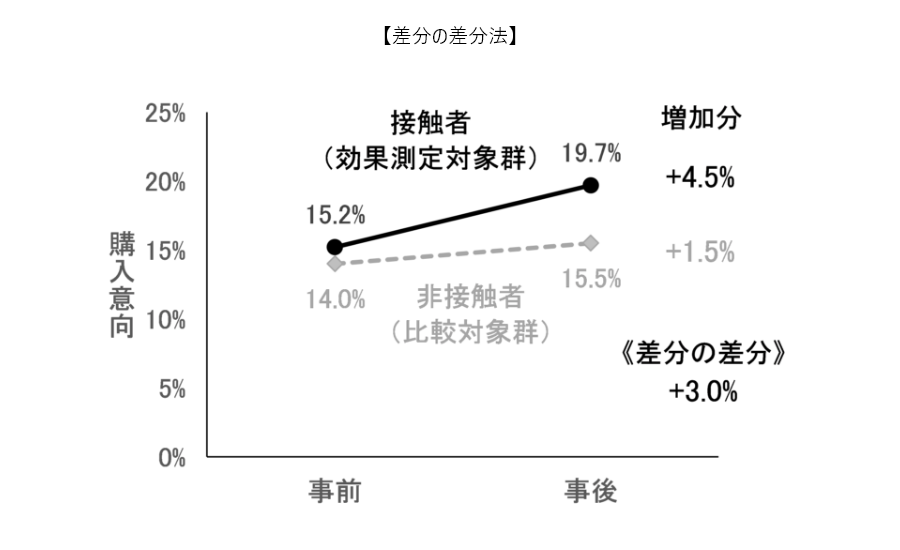
差分の差分法の場合、事前の水準を考慮することで、それぞれの群に入る人々の偏りを補正しましたが、広告接触後に商品を買ったという事後の値しかわからない場合には、差分の差分法は使えません。
②傾向スコア
「効果測定対象群」と「比較対象群」に含まれるサンプルの構成を“均質”にすることで、各群の偏りを補正しようという考え方です。
広告効果の推計の例でいうと、広告接触者群（効果測定対象群）では女性の比率が高くなり、広告非接触者群（比較対象群）では女性の比率が低くなります。本来ならば、どちらの群も男女比を１：１で均質化して、商品購入率などの結果を測定し、接触者群と非接触者群の差から広告効果を推定する必要があります。言い換えると、広告接触群の場合は、女性のサンプルには低い重み付けを行って、全体の結果を計算すれば、正しい比較ができるといえるでしょう。
具体的には、女性の広告接触者群に入る割合（確率）が60%だとした場合、広告接触者群にいる女性のサンプルの効果には、その逆数（1/0.6）を重み付け係数としてかけ、反対に広告非接触者群に入る女性サンプルには1/0.4を重み付け係数としてかければ、２つの群のサンプルの偏りを補正できます。
したがって、各サンプルが「広告接触者群（効果測定対象群）に入る確率」が推計できれば、効果を正しく推計できることでき、この確率のことを「傾向スコア」と言います。具体的には、性別、年代、職業などの属性を説明変数として、回帰分析を行うことで、各サンプル別の傾向スコアを求めます。求めたサンプル別の傾向スコアの逆数を、各サンプルの重み付け係数として採用することで、効果測定対象群と比較対象群の結果を均質に比較できるようになり、正しい因果関係を推計できます。この手法を傾向スコアによる「逆確率重み付け推定法（Inverse Probability Weighting：IPW）」と言います。
ただし、正しく推計するためには、２つの群を均質化するための要素（性別、年代、職業など）が正しく選定されている必要があり、その要素から効果測定対象群に含まれる確率（傾向スコア）が正しく計算されている必要があり、まだ課題は多くあります。
“相関”ではなく“因果”を正しく把握しようとする「因果推論」は、まだ研究途上であり、統計学の中でも最先端のテーマです。データの量、無作為性などの制約もあり、完全な因果関係を把握しにくいのも事実です。２つのデータの関係をみる「回帰“分析”」に対して、「因果“推論”」という名前がついていることが、因果関係を把握することの難しさを象徴しているかもしれません。
関連記事
「因果推論」に関して動画でお伝えしています
このページを見ている人はこんな用語解説ページも見ています
「因果推論」に関してこんなページも見られています
Information Rules（邦訳「情報経済の鉄則」）
（邦訳「情報経済の鉄則」） 2019/09/04 前回取り上げた 「予測マシンの世紀」 の源流といえる「情報経済」を既存の経済学で読み解いた古典的名著。ほぼ20年前の1998年の時点で、現在のGAFA的なプラットフォーマーの登場はすでにこの本で予見されていた。著者の一人であるハル・ヴァリアンは2002年からGoogleの経済学のブレーンを務めている。そして今、
番外編】2019年ノーベル経済学賞とDX（前編） 2019/10/15 10月14日、今年のノーベル経済学賞受賞者が発表された。受賞理由は貧困削減を目指す開発経済学の分野に「ランダム化比較試験（RCT : Randomized Controlled Trial）」という新たな手法を取り入れ、開発プログラムの政策効果を飛躍的に向上させた功績が評価されたことにある。
番外編】2019年ノーベル経済学賞とDX（後編） 2019/10/18 2019年のノーベル経済学賞には、貧困問題の解決にRCT（ランダム化比較試験）やフィールド実験などの科学的手法を導入したエステル・デュフロ教授らが選ばれた。このRCTやフィールド実験、そして因果推論といった「因果関係をきちんと抽出できる分析手法」が近年急速に発展している。ビッグデータという言葉が登場して久しいが、
金融ITフォーカス 2018年9月号
数理の窓 因果関係への挑戦 松本 ゆかり 「丈の短いスカートが流行している年は景気が良くなる」という法則は、景気動向に関する俗説として知られている。スカートの丈と景気に偶然の相関関係はあるのだろうが、そこに因果関係があると本気で信じている人は少ないだろう。因果関係とは原因と結果の関係のことで、ここではもちろん、「原因＝スカートの丈」、「結果＝景気」である。 発行形式 発行時期 毎月5日発行