P値とは
統計学における「仮説検定」(自分が設定した仮説が正しいかどうかを統計的に判定する方法)において、元データの指標が、サンプルから観察された値と等しいか、それよりも大きな(小さな)値をとる確率のこと。P値のPは確率を表すProbabilityのP。
仮説検定におけるP値の計算方法
統計的仮説検定の場合は、自分が設定した仮説と反対のことを棄却することで、自分の仮説が正しいことを証明します。
例えば、A群の平均値とB群の平均値には「差がある」ことを証明したい場合には、A群の平均値とB群の平均値には「差がない」という仮説をたて、それが間違っていることを証明します。差がないという仮説を棄却することで、差があることを証明するのです。
A群とB群の中から、サンプルを抽出して平均値を計算し、2つの平均値の差を計算します。A群とB群の平均値には「差がない」とした場合に、サンプルから実測された平均値の差が起こる確率を求めます。A群・B群のデータが正規分布に従うなどの前提があれば確率を計算することができます。
P値とは、特定の値になる確率ではなく、それよりも大きくなる確率(実測された差よりも大きな差になる確率)です。その値が小さければ、実測された差よりも大きくなる確率はめったにないため、仮説が棄却されます。どれぐらい小さい場合に棄却してよいかを決める水準を「有意水準」とよび、一般的には0.05をとることが多いですが、目的に応じて水準を設定する必要があります。
回帰分析におけるP値
ビジネスの場面では、P値は、回帰分析の結果として表示されることが多いでしょう。
エクセルなどの計算では、回帰分析結果として、以下のようなアウトプットが出てきます。
このP値の見方についても解説しておきます。
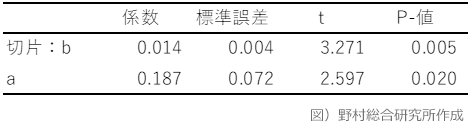
XとYのデータ群があった時に、XとYの関係を、Y=a・X+bのような式で表すことが回帰分析です。XとYのデータから、最も誤差が少なくなるような形でaとbを推計します。その結果、係数aは0.187と計算され、この係数aの確からしさ(有意性)を検定した結果が「t」(t値とも表現される)と「P-値」(P値とも表現される)です。
検定の対象となる仮説は「XとYは関係がない(aがゼロ)」とし、この仮説を棄却できれば、XとYの間には「回帰係数aという関係がある」という考え方をします。回帰分析は、XとYのサンプルデータの組み合わせから、XとYの元にある関係を推計しようという考え方です。計算された結果は、正規分布に類似している「t分布」になることがわかっており、この性質をもとに検定(「t検定」と呼ばれる。)を行います。t検定では、「t値」と呼ばれる「検定統計量」をもとに仮説の確からしさを検定します。
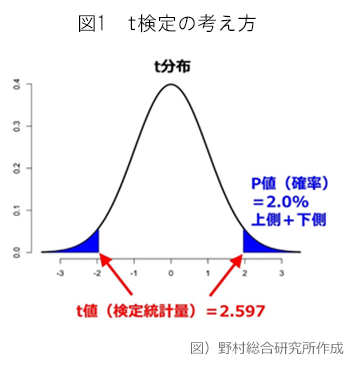
今回の表では、係数aのP値は0.020となっており、有意水準を0.05とした場合には、仮説(aがゼロになる)が棄却されます。したがって、仮説検定の結果、aが0.187と計算された結果は、間違えているとは言えないと判断できます。
仮にP値が0.05より大きくなる場合は、仮説は棄却されず、aが0になる可能性があるため、その仮説の前提になった係数aの値は、統計的には、正しいとは言えません。
P値で確からしさを判断する場合の注意点
P値の結果だけでは、必ずしも判断できない場合があります。それは、P値のもとになるt値は、サンプル数の影響を大きく受けるためです。今回の検定統計量であるP値は以下のように計算されます。
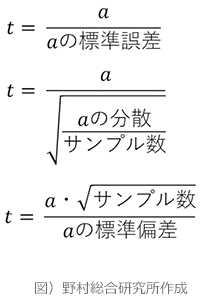
すなわち、t値はサンプル数が大きくなるほど、大きくなる傾向にあります。t値が大きくなるとP値は小さくなるため、aが0になるという仮説が棄却されやすくなり、Y=a・X+bという回帰分析が正しいという判断がされやすくなります。
近年は、ビッグデータなどの活用により、莫大なサンプル数でt値を計算することが増えたため、aの大きさや、aのバラツキ(標準偏差)によらず、P値をみるだけ、回帰分析の結果が正しいと判断されがちなため、注意することが必要です。