モデル評価指標とは
モデル評価指標とは、ある「予測モデル」の精度を定量的に計測し、相互比較を可能とするものです。近年、普及が進む機械学習技術においても、コンピュータが機械的にモデルを最適化する際にモデル評価指標が用いられています。
データサイエンス技術を用いて何らかの「予測モデル」を生成した際に、そのモデルの性能（予測精度）を定量的に計測することが期待されます。モデル評価指標とは、このモデル性能を測るための計算式です。一般にデータサイエンス技術を用いて「予測モデル」を開発する際は、まずこのモデル評価指標と目標値を定め、その数値を達成するためにモデリングの試行錯誤を行うというアプローチを取ります。
代表的なモデル評価指標
予測モデルには、大きく「回帰（値を予測する）モデル」と「分類（真か偽かを予測する）モデル」があります。それぞれの具体的なモデル評価指標としては、以下のようなものが挙げられます。これらは代表例ですが、これら以外にも非常に多くの種類のモデル評価指標があります。また、モデルが解決したい課題の性質に合わせて、オリジナルのモデル評価指標を新たに定義することもあります。
＜回帰モデル＞
| 評価指標名 | 説明 |
|---|---|
| MAE(平均絶対誤差) | 誤差の絶対値を平均したもの |
| MAPE(平均絶対パーセント誤差) | 誤差の絶対値÷実際の値を平均したもの |
| WAPE(加重絶対パーセント誤差) | 誤差の絶対値÷実際の値を、実際の値で重み付けして平均したもの（MAE÷実際の値の平均と等しい） |
| MSE(平均二乗誤差) | 誤差の二乗を平均したもの |
| RMSE(平均二乗誤差の平方根) | MSEの平方根を取ったもの |
＜分類モデル＞
| 評価指標名 | 説明 |
|---|---|
| 正解率 | 全ケースのうち正解(予測・実際とも真、または、予測・実際とも偽)の割合 |
| 適合率 | 真と予測したもののうち、実際も真の割合 |
| 再現率 | 実際が真のもののうち、真と予測した割合 |
| F1スコア | 適合率と再現率の調和平均 |
| logloss(対数損失) | 実際が真(1)のものは-log(p)、偽(0)のものは-log(1-p)で求めた値の平均 |
回帰モデルの評価指標としては、計算の分かりやすさもあり、MAE、MAPEがよく用いられます。ただし、これらの指標には欠点もあり、MAEは小さな値の誤差が見えにくい指標であり、逆にMAPEは小さな値の誤差に影響されやすい指標です。重み付けによりこれらのバランスを取った指標がWAPEです。MSEは二乗するために計算が容易であるという特長がありますが、単位が消えるという欠点があります。RMSEは、その平方根を取ることで、MSEを元の単位に戻そうとするものです。なおRMSEは二乗の平均を取った後に平方根を取るという計算上の理由により、MAEと比べると大きな誤りがより重視される特性があります。
分類モデルの評価指標には、シンプルな指標として全ケースを分母として正解の割合を求める正解率があります。適合率や再現率は、真をどれだけ当てられたかに着目し、予測を分母とするか実績を分母とするかの違いでそれぞれ表現します。ただし、これら3つの指標は、いずれも真偽に偏りがある場合に適切に評価できないという課題があります。F1スコアはこれらをバランスよく評価する指標であり、適合率と再現率の調和平均(*)で求められます。logloss(対数損失)は、機械学習技術で一般的に用いられ、予測値の変化に合わせて、連続的に誤差が変化する特性があります。
- (*)
調和平均は、「平均」の一種であり、各要素の逆数の平均を取り、さらにその逆数を取ることで計算します。生産性の平均と説明されることもあります。
機械学習とモデル評価指標
一般的な機械学習技術においても、このモデル評価指標を設定する必要があります。機械学習技術では、モデル評価指標が最も良くなるように、指標の改善が飽和するまで大量の演算を繰り返してモデルを自動的に構築します。計算の効率性の観点などから、回帰モデルではMSE、分類モデルではlogloss(対数損失)がよく用いられます。なお、機械学習の分野ではモデル評価指標の代わりに「損失関数」と呼ばれることもあります。
例えば、logloss(対数損失)は、予測された確率が実際の値と比べ、どれだけ外れていたかを示す指標です。計算式としては、実際の値が真のものは、-log(真の予測確率)、偽のものは、-log(1-真の予測確率)として求めます。予測精度が高いモデルほどlogloss値は小さくなり、完全に正解を当てられるモデルはlogloss値が0になります。予測確率を横軸、logloss値を縦軸に取ると、下図のようなグラフになります。
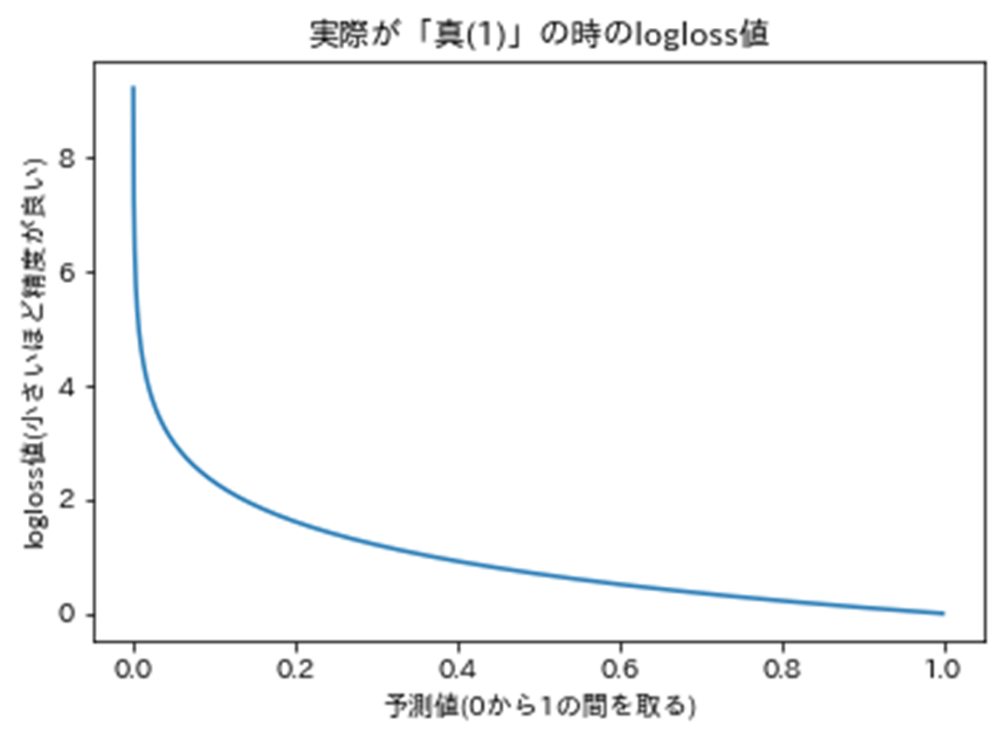
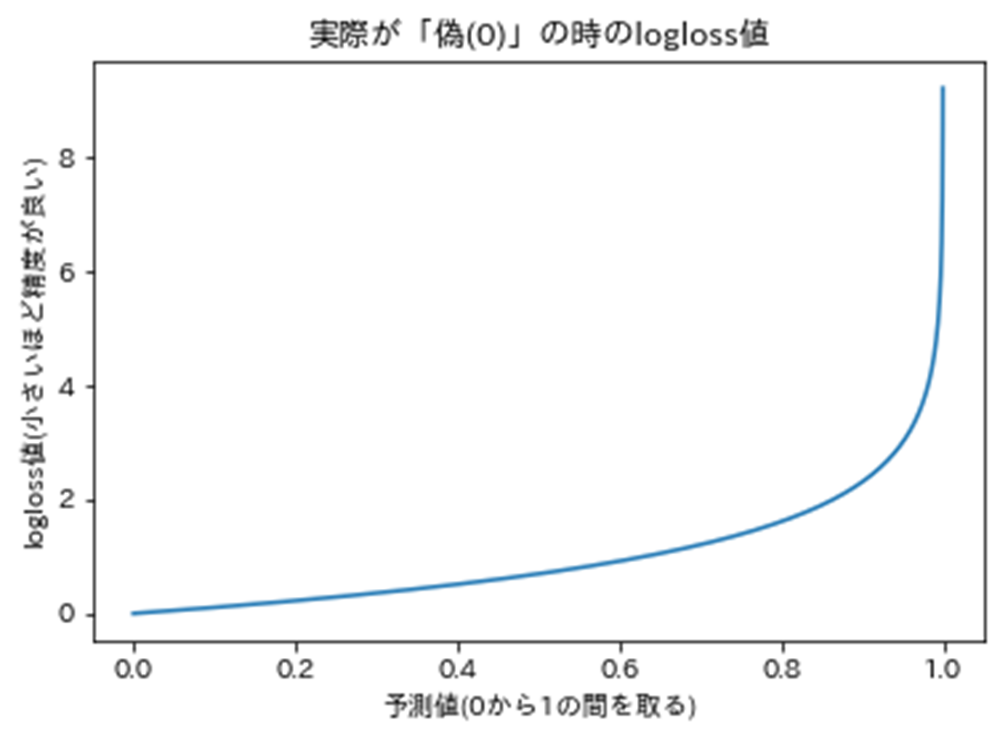
具体的な計算例として、以下のように、「真・真・偽・偽」4つのケースについて、それぞれ真である確率が「80%・30%・15%・95%」と予測した場合のloglossを算出してみます。
ケース1は、真である確率が80%と予測して実際に真ですので、誤差は「0.2」となり、logloss値は、-log(0.8)=0.22となります。ケース2は、真である確率が30%と低く予測したため、誤差は「0.7」と大きくなり、logloss値も、-log(0.3)=1.20と大きくなります。ケース3は、真である確率が15%と低く予測して実際も偽ですので、誤差は「0.15」となり、logloss値は、-log(0.85)=0.16となります。ケース４は、真である確率が95%と高く予測したため、誤差は「0.95」と大きくなり、logloss値も、-log(0.05)=3.00と大きくなります。なお、この場合モデル全体のlogloss値はこれらの平均値を取り、1.15となります。
logloss(対数損失)の計算例
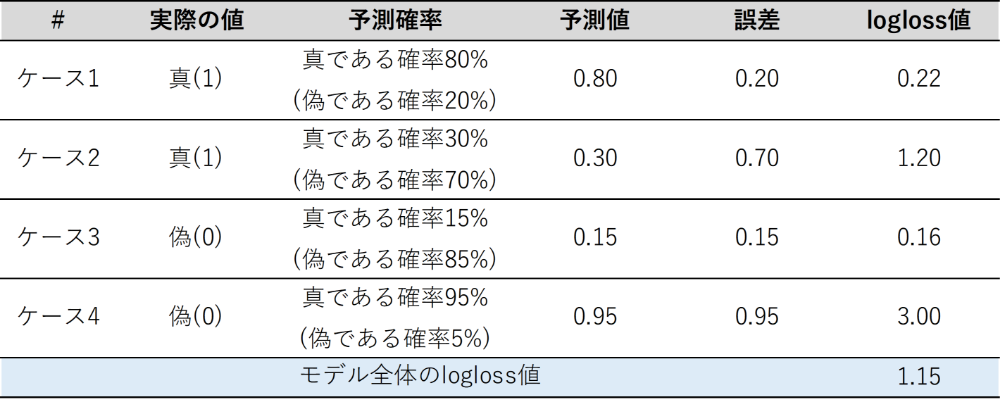
logloss(対数損失)は、正解時の誤差は0ですが、不正解時の誤差が非常に重く（∞）なります。不正解に近付くにつれてペナルティが加速度的に重くなることから、機械学習においては、予測を外した場合に、大幅に（効率的に）パラメータが修正されやすく、計算効率が良いというメリットもあります。
関連記事
「モデル評価指標」に関して動画でお伝えしています
このページを見ている人はこんな用語解説ページも見ています
「モデル評価指標」に関してこんなページも見られています
攻めの「データガバナンス」で企業価値を高めてDXを成功に導け
DX（デジタルトランスフォーメーション）の一環で、データ解析や機械学習を用いて新しいサービスや事業を立ち上げようとしても、実際にデータを使う段階で壁にぶつかり、「思うように成果を出せずにいる企業が増えている。信頼されるデータ活用の仕組みづくりに早く取り組むことが、競争優位性を確立できる」と、野村総合研究所（NRI）システムコンサルティング事業本部の土屋明義と渡辺文明は指摘します。その解決策となる「攻めの」データガバナンスとは、どのようなものでしょうか。
GPG-Autoソリューション 自動車メーカーの視点 自動車メーカの視点 車両データを活用した新たな事業モデルの構築「コネクテッドサービス開発支援」 コネクテッド化の進展に伴い、新たな事業機会が登場。幅広い検討 スコープから、自社のポジショニングとエコシステム構築が必要です。 2025年には、新車の7割以上がコネクテッド化。収集データの活用先は幅広い センシング、通信、
こんにちは、野村総合研究所 システムデザインコンサルティング部の清水です。 データ分析PoCや機械学習モデルを活用したシステム導入支援などを行っています。 今回は社内のデータサイエンティストのスキルアップを目的に、社内データ分析コンペティションを活用した取り組みついてご紹介します。